As we’ve already discussed, prime factorization is cool, but highly inefficient when it comes to determining if an extremely large number is prime. So here comes an introduction about the Solovay-Strassen primality test.

That looks fancy, but bear with me, I’m gonna break this down really small so it’s easier to understand.

The actual algorithm

If you google this test, you’ll see something like this. Though I’ll be nice and slightly clean it up

def is_prime(n, iterations):
    for i in range(iterations):
        a = random(2, n-1)
        x = 
        if x == 0 or :
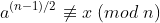            return "composite"
    return "probably prime"

Now here’s the big question, what does any of that mean? I pinkie promise that I’ll explain everything here and soon enough you’ll understand what’s going on and how you can write this code yourself, if you actually wanted to do so.

Before we do math

There will be posts after this where we dig into the math of this and explore what all this means. Before we get into that, I just wanna talk a teeny bit about this algorithm.

This is called a probabilistic algorithm meaning that statistically speaking, if it says \(n\) is prime, there’s a very high likelihood it is, but that’s not a guarantee. Most algorithms you interact with will be 100% accurate when with it’s output. But for this one, you can pass in the same value of \(n\) multiple times and get different results due to the randomness of it.

Obviously it would be great if we could use a deterministic algorithm, but the deterministic versions are highly inefficient compared to probabilistic ones, like this. Like I said before, with this problem, we have trade-offs of complexity and certainty. And we’re going to explore and understand those trade-offs more as this series continues.